14.08.2015 | Wie groß ist das Universum bzw. welche Größe hat das beobachtbare Universum? … Das ist eine Frage, die alles andere als leicht zu beantworten ist. Unter anderem, weil zunächst viele grundlegende Parameter erklärt werden müssen. Aber, ich versuche es trotzdem:
Nach neuestem Kenntnisstand der Wissenschaft hat sich das Universum vor 13,8 Milliarden Jahren mit dem Urknall in seine Existenz gestürzt (Materie, Raum und Zeit sind dabei aus einer ursprünglichen Singularität entstanden). Um nun fortzufahren, muss erst mal der Begriff „Beobachtbares Universum“ erklärt werden. Nach dem Standardmodell der Kosmologie ist es derjenige Teil, der von einem beliebigen Ort aus (z.B. der Erde) kugelförmig in alle Richtungen unserer Beobachtung zugänglich ist. Da nichts schneller als das Licht ist, würde man für diesen Radius ein Ausmaß von genau 13,8 Milliarden Lichtjahren vermuten und somit sagen: „Wir sehen rings um uns Objekte bis in eine Entfernung von 13,8 Milliarden Lichtjahre“. (Anmerkung: 1 Lichtjahr entspricht einer Strecke von rund 10 Billionen Kilometer).
Doch diese Vermutung ist nicht korrekt. Denn dieser Radius weist nämlich eine Ausdehnung von gut 46 Milliarden Lichtjahren auf – also dreimal so groß. Man nennt diesen Radius auch Partikelhorizont oder Beobachtungshorizont. Berechnet wird er unter Berücksichtigung der Materiemenge des Universums, Einsteins kosmologischer Konstante und der Hubble-Konstante (siehe unten).
Kurzum: Wir können heute zwar Licht sehen, das von Atomen vor mehr als 13 Milliarden Jahren ausgesendet wurde (genauer gesagt einige hunderttausend Jahre nach dem Urknall) und somit auch gut 13 Milliarden Jahre alt ist. Allerdings sind genau diese Atome, die damals dieses Licht entsandten, heute viel, viel weiter weg von uns – nämlich nicht 13,8 Milliarden Lichtjahre, sondern eben 46 Milliarden Lichtjahre.
Derzeit beträgt der beobachtbare Radius also 46 Milliarden Lichtjahre!
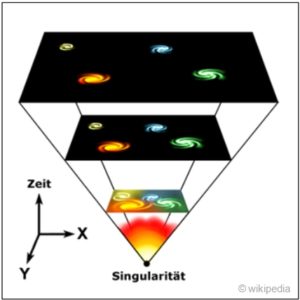
Schuld an dieser Diskrepanz ist die kontinuierlich beschleunigte Expansion des Universums seit dem Urknall (die wiederum die Dunkle Energie zu verantworten hat – so die derzeitige Lehrmeinung). Aber Achtung: es fliegt seit dem Urknall nicht alles von einem ehemals zentralen Punkt aus davon, sondern es dehnt sich dabei der Raum selbst aus! Siehe dazu die nebenstehende Grafik.
(Randnotiz: Die Grafik müsste allerdings so korrigiert werden, dass die Galaxien in der ersten Ebene rötlicher und von ihrer Struktur her auch anders dargestellt werden, als die Galaxien in der obersten Ebene, die den Jetztzustand des Universums zeigen. Denn von uns aus weit entfernte Galaxien erscheinen nicht nur sehr rotverschoben, sondern sahen nach dem Urknall auch anders aus, als heute. Sie Durchlaufen eine Entwicklung, bei der sich Struktur und Form über die Zeit verändert).
Was ganz wichtig ist: Der Urknall ist nicht ein Punkt im Weltall, auf den man von der Erde aus schauen kann. Der Urknall ist vielmehr überall. In jeder Richtung und an jedem Ort. Also beispielsweise auch in Ihrer Hosentasche oder in Nachbars Garten.
Gut vorstellen kann man sich das expandierende Universum mithilfe eines Rosinen-Kuchen. Nicht die Rosinen dehnen sich beim Backen im Ofen aus, sondern der Teig (= der Raum) dazwischen. Eine andere Möglichkeit ist es, sich einen aufgeblasenen Luftballons vorzustellen, auf dessen Hülle man mehrere Punkte im jeweils immer selben Abstand malt und den Ballon dann weiter aufbläst. Alle Punkte entfernen sich dann immer weiter und schneller voneinander, wenn man den Ballon weiter aufbläst. (Randnotiz: Das Universum entspricht der Hülle des Ballons).
Das wiederum bedeutet, dass die 46 Milliarden Lichtjahre, die der Radius (=Partikelhorizont) des beobachtbaren Universums misst, nur für die Jetztzeit gilt! Denn weil sich das Universum kontinuierlich beschleunigt ausdehnt, wächst der Partikelhorizont immer noch weiter an – und zwar unbegrenzt. Derzeit beträgt der Radius für das beobachtbare Universum eben 46 Milliarden Lichtjahre. Und er gilt selbstverständlich für jeden Standort innerhalb des Universums gleichermaßen; nicht nur für die Erde. Jeder Punkt im Universum hat seinen eigenen (jedoch stets gleich großen) Partikelhorizont. Stehen sich zwei solcher Punkte nahe genug, überschneiden sich ihre jeweiligen Partikelhorizonte natürlich. Sie sehen also Teile des selben Raumes.
Welches entsandte Licht können wir dann nicht mehr sehen?
Nun wird es etwas anspruchsvoller … Dazu müssen wir uns zunächst einen wesentlichen Sachverhalt genauer ansehen. Nämlich das bereits erwähnte Luftballon-Modell, das wir in das Universum übertragen. Stellen Sie sich vor, wir haben vier Punkte. Der eine Punkt repräsentiert die Erde, die anderen drei jeweils eine Galaxie. Die Entfernungen dazwischen seien jeweils immer genau ein Lichtjahr groß. Stellen Sie sich nun weiter vor, wir lassen den Raum mit einer Geschwindigkeit von 50 km/s ausbreiten. Folglich entfernt sich Galaxie A von der Erde mit 50 km/s. Galaxie B entfernt sich von Galaxie A ebenso mit 50 km/s. Und Galaxie C entfernt sich von Galaxie B natürlich auch mit 50 km/s. Aber: Aus Sicht der Erde entfernt sich die Galaxie B nicht mit 50 km/s, sondern mit 50 km/s + 50 km/s (= 100 km/s); also doppelt so schnell. Und Galaxie C entfernt sich aus Sicht der Erde sogar mit 50 km/s + 50 km/s + 50 km/s. Also dreimal so schnell.
Überträgt man das in eine Formel, so ergibt sich immer eine Konstante, wenn wir die Geschwindigkeit, mit der sich zwei Punkte aufgrund der Raumausdehnung voneinander entfernen, durch deren Abstand teilt. Und genau das beschreibt der sogenannte Hubble-Parameter H (t). Von der Hubble-Konstante spricht man dann, wenn man für das (t) das jetzige Alter des Universums einsetzt (also 13,8 Milliarden Jahre). Dieser Hubble-Parameter hat derzeit einen Wert (der auch durch Messungen im Weltall bestätigt ist) von ca. 70 Kilometer pro Sekunde pro Megaparsec (1 Megaparsec entspricht etwa 3 Millionen Lichtjahre).
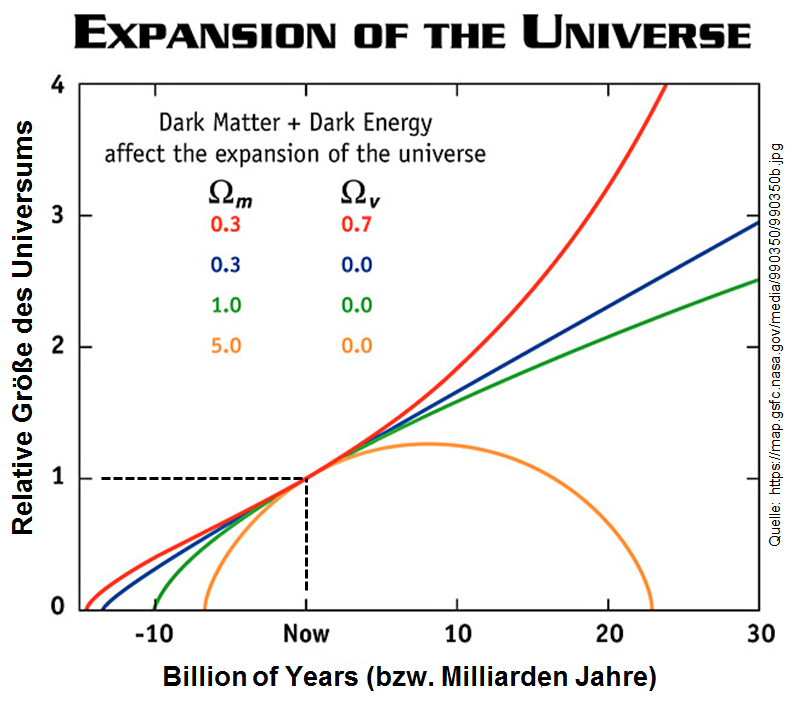
Aufs All bezogen bedeutet dieser Wert: Zwei Galaxien, die im Abstand von 1 Megaparsec zueinander stehen, entfernen sich aufgrund der derzeitigen Expansion des Alls mit 70 km/s relativ voneinander. Der Hubble-Parameter ist eine Funktion der Zeit. Sein Wert H war unmittelbar nach dem Urknall (nämlich in der Inflationsphase des Universums) extrem (!) groß. Danach wurde H schnell kleiner und im weiteren Verlauf dann sukzessive noch kleiner (verzögerte Expansion). Seit etwa 1 Milliarde Jahre nimmt der Wert H allerdings wieder zu (beschleunigte Expansion). Dieser gesamte Verlauf ergibt sich auf Basis der sogenannten Friedmann-Universen. Im nachfolgenden Diagramm ist es die rote Kurve. Die Steigungen der vier Kurven entsprechen dem Hubble-Parameter H(z). (Randnotiz: zeitgleich, aber unabhängig davon, wird ein anderer Wert immer größer. Nämlich die sogenannte Hubble-Sphäre, die ich Ihnen gleich vorstellen werde).
Wir gehen einen Schritt weiter: Licht breitet sich im Vakuum bekanntlich mit Lichtgeschwindigkeit aus – also mit rund 300.000 km/s. Die Frage ist nun: wie schnell muss sich ein Raumvolumen, in das eine Galaxie eingebunden ist, von uns entfernen, dass uns das Licht dieser Galaxie auf der Erde nicht mehr erreicht? Logischerweise muss sich das Raumvolumen mit Lichtgeschwindigkeit von uns entfernen! Zwar kommt das Licht der Galaxie immer noch mit Lichtgeschwindigkeit auf uns zu; doch gleichzeitig fliegt die Quelle des Lichtes, nämlich die Galaxie, mit Lichtgeschwindigkeit von uns weg. In diesem Fall erreicht uns auf der Erde von dieser Galaxie kein Lichtteilchen (Photon) mehr. Denn durch die Expansion des Raumes sind diese Photonen „unendlich rotverschoben“ und damit „unendlich dunkel“. Die beiden Licht-Geschwindigkeiten heben sich also nicht zu Null auf (was ein Widerspruch zu Einsteins Theorie wäre), sondern das Licht, das uns erreicht, ist schlichtweg durch die Expansion des Raumes zu dunkel, als dass wir es noch sehen und messen könnten. (Randnotiz: natürlich ist auch keine Addition von Lichtgeschwindigkeiten möglich. Ein Laserstrahl bewegt sich beispielsweise nicht plötzlich mit doppelter Lichtgeschwindigkeit fort, wenn man ihn in Fahrrichtung aus einem Zug „abfeuert“, der selbst mit Lichtgeschwindigkeit unterwegs ist. Lichtgeschwindigkeit + Lichtgeschwindigkeit = Lichtgeschwindigkeit).
Diese starke Rotverschiebung sehr weit entfernter Galaxien sieht man übrigens auch sehr gut auf dem sogenanten Hubble Deep Field. Also dem Foto, dass das Hubble Weltraumteleskop 1995 von einem gerade nur rund 2 Vollmondscheiben großen Durchmesser im Sternbild Großer Bär machte, auf dem nach fertigstellung über 3000 Galaxien gut bis sehr gut erkennbar waren. Je weiter die Galaxien entfernt waren, desto kleiner, röter und strukturloser waren sie auf dem Foto zu sehen (Randnotiz: das Hubble Deep Field enthielt noch entfernte Galaxien mit einer Rotverschiebung von z=6, was einer Entfernung von 12 Milliarden Lichtjahten entspricht).
Doch zurück zum Thema: Wir können nun genau die zugehörige Entfernung berechnen, bei der genau dieser Fall eintritt, dass uns gerade kein messbares Licht mehr von dort erreicht. Und zwar: Hubble-Radius D (t) = Lichtgeschwindigkeit geteilt durch Hubble-Parameter H (t). Also: 300.000 km/s geteilt durch 70 km/s pro Megaparsec = 14 Milliarden Lichtjahre.
Die Hubble-Sphäre & Überlichtgeschwindigkeit
Wie wir soeben berechnet haben ist eine Galaxie, die sich gerade mit der Lichtgeschwindigkeit entfernt, also etwa 14 Milliarden Lichtjahre von uns entfernt. Und das gilt natürlich auch ganz allgemein: alle Objekte, die genau diesen Abstand zu uns haben, entfernen sich von uns mit Lichtgeschwindigkeit. Dort ist also die Fluchtgeschwindigkeit gleich die Lichtgeschwindigkeit. Und zu diesem Abstand bzw. Radius sagt man Hubble-Sphäre (hubble sphere) oder auch Hubble-Radius.
Beschrieben wird er durch eine Kugel. Alle Objekte innerhalb dieser Kugel entfernen sich mit Unterlichtgeschwindigkeit von uns, alle genau auf der Kugelfläche mit Lichtgeschwindigkeit und alle Objekte jenseits der Kugelfläche mit Überlichtgeschwindigkeit. Das scheint zunächst ein Widerspruch zu Einsteins Spezieller Relativitätstheorie zu sein, die ja besagt, dass die Lichtgeschwindigkeit eine Konstante ist und es nichts geben kann, dass schneller als Licht ist. Doch wie oben schon erwähnt, widerspricht eine überlichtschnelle Raum-Expansion nicht der Einsteinschen Theorie. (Randnotiz: rein formal betrachtet, gibt es keine Überlichtgeschwindigkeit. Doch wendet man das Hubble-Gesetz auf sehr rotverschobene Galaxien an, dann kommt es rechnerisch zu Überlichtgeschwindigkeit).
Der Ereignishorizont
(Radius = 16 Milliarden Lichtjahre)
Vermutlich ist jetzt dann gleich die Verwirrung perfekt. Denn nun müssen wir uns auch noch den sogenannten Ereignishorizont (event horizon) ansehen. Dieser befindet sich außerhalb der gerade beschriebenen Hubble-Sphäre (Radius = 14 Milliarden Lichtjahre), aber noch innerhalb des beobachtbaren Universums (Radius = 46 Milliarden Lichtjahre). Im Standardmodell der Kosmologie liegt der Radius dieser Hubble-Sphäre bei einer Entfernung von gut 16 Milliarden Lichtjahren. Dieser Horizont existiert, weil sich das Universum nicht nur ausdehnt, sondern beschleunigt ausdehnt. Und er sagt uns quasi etwas über die Zukunft. Nämlich, wie weit ein Objekt heute maximal von uns entfernt sein darf, so dass uns sein Licht irgendwann in der unendlichen Zukunft prinzipiell erreichen kann.
Man könnte nun vermuten, dass dieser Ereignishorizont mit der Hubble-Sphäre zusammenfällt, weil uns Lichtteilchen nie erreichen können, wenn sie in einem Bereich ausgesendet werden, der sich mit „Überlichtgeschwindigkeit“ von uns entfernt, nämlich jenseits der Hubble-Sphäre (Sie erinnern sich: hier ist dann die kosmologische Rotverschiebung unendlich). Aber: da die Hubble-Sphäre zukünftig noch ein wenig anwachsen wird, können manche Lichtteilchen wieder in den Bereich innerhalb der Hubble-Sphäre „hineinrutschen“. Die Entfernung, bei der sich Objekte gerade mit Lichtgeschwindigkeit von uns entfernen (also die Hubble-Sphäre) liegt dann nicht mehr wie heute bei 14 Milliarden Lichtjahren Radius, sondern bei 16 Milliarden Lichtjahren. Ein Lichtteilchen (Photon), dass sich damals genau auf der Hubble-Sphäre befand, liegt nun auf einmal in einem Bereich, in dem sich der Raum mit deutlich Unterlichtgeschwindigkeit von uns entfernt. Und so kann uns das Lichtteilchen dann doch erreichen, obwohl sich die Galaxie, die es einst entsendet hat, mit Lichtgeschwindigkeit oder gar „Überlichtgeschwindigkeit“ von uns entfernt hat oder immer noch entfernt. Das ist mit „hineinrutschen“ gemeint. (Randnotiz: leider ist auch die Sache mit der „zukünftig noch ein wenig anwachsenden Hubble-Sphäre“ nicht ganz so eindeutig. Denn ob die Hubble-Sphäre anwächst oder abnimmt hängt davon ab, welches Maß man für die Zeit nimmt (kosmische Zeit oder konforme Zeit) und welches für die Entfernung (Eigendistanz oder mitbewegte Entfernung. Das macht die ganze Angelegenheit leider ziemlich kompliziert und somit auch den Versuch, es zu erklären und zu beschreiben).
Licht, das jetzt von Galaxien ausgesendet wird, die sich jenseits des Ereignishorizontes befinden (also somit jenseits des Radius von 16 Milliarden Lichtjahren), kann uns auf der Erde niemals erreichen, weil der Raum zwischen der Galaxie und uns einfach zu schnell expandiert.
Kurzum: Wir können also nur diejenigen Ereignisse in einer Galaxie von der Erde aus sehen, die in dieser Galaxie vor dem Überschreiten des Ereignishorizontes stattgefunden haben.
Es gilt ganz allgemein: Objekte und Ereignisse jenseits des Ereignishorizontes stehen in keiner kausalen Verknüpfung mehr mit uns, so dass uns von dort keine Informationen mehr erreichen können. Dies gilt auch in umgekehrter Richtung.
Da der Ereignishorizont nicht unbegrenzt wächst (Randnotiz: er nähert sich vielmehr einem Grenzwert an; siehe nachfolgende Grafiken), überschreiten alle Objekte irgendwann den Ereignishorizont (event horizon), weil die Entfernungen zwischen den Objekten aufgrund der Raum-Expansion unbegrenzt wachsen. Dies gilt allerdings nicht für alle gravitativ an unsere Umgebung gekoppelte Objekte. Das sind diejenigen, die sich in einer Entfernung von ein paar Millionen Lichtjahren aufhalten – also alle Galaxien der lokalen Gruppe. Mit diesen werden wir in etwa 100 Milliarden Jahren alleine sein. Alles andere liegt dann nämlich schon hinter dem kosmischen Ereignishorizont.
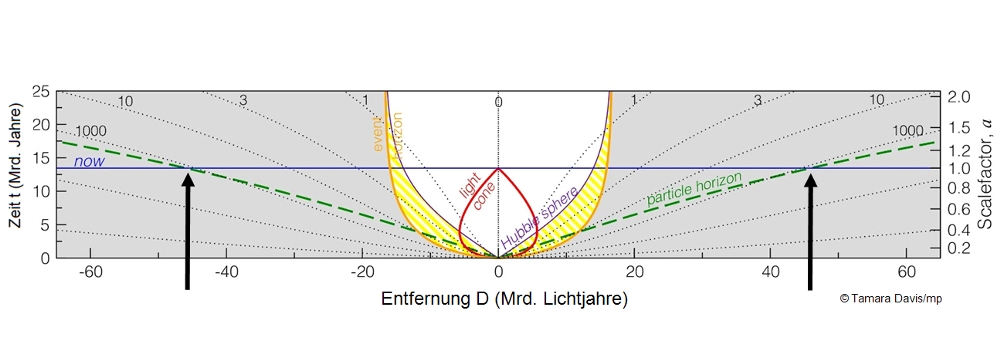
Hier eine animierte Version:
Und was genau bedeuten nun diese 46 Milliarden Lichtjahre Radius des beobachtbaren Universums?
Es bedeutet, dass wir Licht von Galaxien sehen, die heute zwar 46 Milliarden Lichtjahre entfernt von uns sind. Doch als sie dieses Licht seinerzeit ausgesendet haben, waren Sie viel näher an der Erde. Nämlich nur 40 Millionen Lichtjahre entfernt (das kann man berechnen). Andererseits bedeutet es, dass wir einen Lichtblitz, den ein Objekt in einer Entfernung von 46 Milliarden Lichtjahren in diesem Moment aussendet, niemals sehen können. Und es bedeutet ebenso, dass alle Objekte, die innerhalb des Radius des beobachtbaren Universums (also innerhalb der 46 Milliarden Lichtjahre) Licht aussenden, von uns nicht zwangsläufig irgendwann einmal gesehen werden. Ist dieses Objekt aber maximal 16 Milliarden Lichtjahre von uns entfernt (und damit innerhalb des kosmischen Ereignishorizontes), können wir Licht, das es jetzt gerade abstrahlt und in Richtung Erde schickt, irgendwann einmal in der unendlichen Zukunft bei uns eintreffen sehen.
Ob wir das Licht eines frisch geborenen oder gerade sterbenden Stern in einer Galaxie sehen können, hängt also davon ab, wie weit entfernt sich diese Galaxie zu genau diesem Zeitpunkt von uns befindet. Passiert das in einem Bereich kleiner als 14 Milliarden Lichtjahren um uns herum (also innerhalb des Hubble-Radius bzw. der Hubble-Sphäre), wird uns das Licht dieses Ereignisses auf der Erde erreichen können.
Am Ende dieseslangen Artikels bleibt mir nur eines zu sagen: Ich habe Sie gewarnt … (dass es durchaus etwas schwierig wird) 🙂
Manuel Philipp
Ergänzung (Juli 2017):
Da wir bei unseren Sternführungen immer wieder gefragt werden, wie weit man denn mit unserem 120 mm Großfernglas (APM 120 SD-Apo Großfernglas) ins Weltall sehen würde: Aufgrund der Objektivöffnung von 120 mm (pro Auge) ergibt sich (bei sehr dunklem und transparentem Himmel) eine Grenzgröße von etwa 13,5 mag (bis knapp 14 mag). Somit sind z.B. einige Quasare zu sehen (also aktive, extrem helle Kerne weit entfernter Galaxien), die von uns ca. 4-5 Milliarden Lichtjahre entfernt sind. Z.B. der Quasar 3C 273, dessen Licht ca. 2,5 Mrd. Jahre unterwegs war bis es uns erreicht hat. Oder, wenn auch an der visuellen Wahrnehmungsgrenze, der Quasar bzw. Blazar 3C 66A, dessen Licht ca. 4,5 Mrd. Jahre unterwegs ist, bis es uns erreicht hat. Wegen der Expansion des Universum sind diese Objekte aber mittlerweile schon weiter weg als 2,5 bzw. 4,5 Mrd. Lichtjahre. 3C 66A nämlich bereits ca. 5,4 Mrd LJ (statt 4,5 Mrd. Lichtjahre). Also eine durchaus beachtlich Leistung für ein solches 120 mm Grossfernglas.